Các phương pháp hồi quy được sử dụng rộng rãi trong nghiên cứu khoa học để phân tích dữ liệu thực nghiệm, xây dựng mô hình dự đoán và kiểm tra giả thuyết. Hồi quy là một phương pháp thống kê được sử dụng để dự đoán giá trị của một biến dựa trên giá trị của một hoặc nhiều biến khác. Đây là một công cụ mạnh mẽ trong phân tích dữ liệu, giúp hiểu mối quan hệ giữa các biến và đưa ra dự đoán chính xác. Trong bài viết này, chúng ta sẽ tìm hiểu về các phương pháp hồi quy phổ biến và cách chúng được áp dụng trong các lĩnh vực khác nhau.
- Hồi Quy Tuyến Tính (Linear Regression)
1.1. Định Nghĩa
Hồi quy tuyến tính là một phương pháp cơ bản trong phân tích hồi quy, được sử dụng để mô hình hóa mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập. Mô hình hồi quy tuyến tính đơn giản có dạng:

1.2. Ứng Dụng
Hồi quy tuyến tính được sử dụng rộng rãi trong nhiều lĩnh vực như kinh tế, tài chính, y học, và khoa học xã hội. Ví dụ, trong kinh tế, hồi quy tuyến tính có thể được sử dụng để dự đoán doanh thu dựa trên chi phí quảng cáo.
- Hồi Quy Đa Tuyến (Multiple Linear Regression)
2.1. Định Nghĩa
Hồi quy đa tuyến mở rộng hồi quy tuyến tính đơn giản bằng cách bao gồm nhiều biến độc lập.
Mô hình có dạng: 
2.2. Ứng Dụng
Hồi quy đa tuyến được sử dụng khi có nhiều yếu tố ảnh hưởng đến biến phụ thuộc. Ví dụ, trong y học, hồi quy đa tuyến có thể được sử dụng để dự đoán nguy cơ mắc bệnh dựa trên nhiều yếu tố như tuổi, cân nặng, huyết áp, và mức đường huyết.
- Hồi Quy Logistic (Logistic Regression)
3.1. Định Nghĩa
Hồi quy logistic là một phương pháp thống kê được sử dụng để mô hình hóa mối quan hệ giữa một biến phụ thuộc nhị phân (chẳng hạn như có/không, đúng/sai) và một hoặc nhiều biến độc lập. Không giống như hồi quy tuyến tính, hồi quy logistic không dự đoán giá trị chính xác mà dự đoán xác suất của một sự kiện xảy ra. Mô hình hồi quy logistic có dạng:
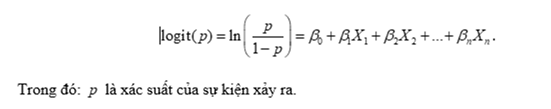
3.2. Ứng Dụng
Hồi quy logistic được sử dụng rộng rãi trong các lĩnh vực y học, khoa học xã hội và tiếp thị. Ví dụ, trong tiếp thị, hồi quy logistic có thể được sử dụng để dự đoán khả năng mua hàng của khách hàng dựa trên các yếu tố như tuổi, giới tính, thu nhập, lịch sử mua hàng, và hành vi trực tuyến. Điều này giúp các công ty xây dựng chiến lược tiếp thị hiệu quả hơn và tăng doanh số bán hàng.
- Hồi Quy Phi Tuyến (Nonlinear Regression)
4.1. Định Nghĩa
Hồi quy phi tuyến được sử dụng khi mối quan hệ giữa biến phụ thuộc và biến độc lập không tuân theo một đường thẳng. Các mô hình hồi quy phi tuyến phổ biến bao gồm hồi quy đa thức và hồi quy logistic phi tuyến.
4.2. Ứng Dụng
Hồi quy phi tuyến được sử dụng rộng rãi trong các lĩnh vực mà mối quan hệ giữa các biến không tuyến tính. Ví dụ, trong khoa học môi trường, hồi quy phi tuyến có thể được sử dụng để mô hình hóa mối quan hệ giữa nồng độ chất ô nhiễm và tác động đến sức khỏe con người.
- Hồi Quy Bayesian (Bayesian Regression)
5.1. Định Nghĩa
Hồi quy Bayesian sử dụng các phương pháp thống kê Bayesian để ước lượng các tham số của mô hình hồi quy. Phương pháp này cho phép kết hợp thông tin từ dữ liệu và các giả định tiên nghiệm để đưa ra các ước lượng.
5.2. Ứng Dụng
Hồi quy Bayesian được sử dụng khi muốn kết hợp thông tin tiên nghiệm và dữ liệu quan sát để đưa ra các dự đoán. Ví dụ, trong y học, hồi quy Bayesian có thể được sử dụng để dự đoán hiệu quả của một loại thuốc mới dựa trên dữ liệu thử nghiệm lâm sàng và thông tin từ các nghiên cứu trước đó.
- Hồi Quy Cây Quyết Định (Decision Tree Regression)
6.1. Định Nghĩa
Hồi quy cây quyết định sử dụng cây quyết định để mô hình hóa mối quan hệ giữa các biến. Mỗi nút trong cây đại diện cho một quyết định dựa trên giá trị của một biến độc lập, và các lá của cây đại diện cho giá trị dự đoán của biến phụ thuộc.
6.2. Ứng Dụng
Hồi quy cây quyết định được sử dụng rộng rãi trong các lĩnh vực yêu cầu dự đoán phức tạp và dễ hiểu. Ví dụ, trong tài chính, cây quyết định có thể được sử dụng để dự đoán rủi ro tín dụng của khách hàng dựa trên thông tin cá nhân và lịch sử tín dụng.
Tóm lại, các phương pháp hồi quy là những công cụ mạnh mẽ trong phân tích dữ liệu, giúp hiểu và dự đoán mối quan hệ giữa các biến. Tùy thuộc vào tính chất của dữ liệu và mục tiêu phân tích, các phương pháp khác nhau có thể được sử dụng để đạt được kết quả tốt nhất. Việc hiểu và áp dụng đúng các phương pháp hồi quy sẽ giúp cải thiện độ chính xác và hiệu quả của các dự đoán, từ đó hỗ trợ quyết định và giải quyết các vấn đề phức tạp trong nhiều lĩnh vực khác nhau.
BỘ MÔN QUẢN LÝ CÔNG NGHIỆP